Problème : Le gâteau

Ce problème contre-intuitif peut se trouver dans un des livres de Peter Winkler. Le problème a été créé par Laurent Lafforgue.

Le gâteau (**)
On prend un gâteau circulaire, de couleur blanc dessus, et noir dessous. On choisit un angle $ 0 \le \alpha \le 2 \pi$ quelconque, et on répète l'opération suivante : on coupe le gâteau devant soi, on tourne le gâteau d'un angle $ \alpha$, on le recoupe devant soi, et on retourne la part qu'on vient de couper.
Montrer qu'après un nombre fini d'étapes, le gâteau redevient blanc dessus.

Le point très surprenant est que ça marche même si $\alpha$ est incommensurable par rapport à $ \pi$ ! Le truc vient du fait qu'on retourne les parts à chaque fois. Quand on y réfléchit, cette opération n'est pas si simple à décrire que ça, surtout quand la part est déjà de plusieurs couleurs... En revanche, il existe des cas où le gâteau ne devient jamais totalement noir dessus.

Commençons par montrer qu'on ne fait qu'un nombre fini de coupes, c'est à dire qu'à partir d'un moment, on repasse sur des coupes déjà faites. Si on place l'origine du gâteau là où est le couteau à chaque étape, l'ensemble des coupes faites à l'étape $ n$ est une liste de nombre compris entre $ 0$ et $ 2 \pi$. Si $ \alpha $ est petit par exemple, on obtient $$ C_0 = \{ 0 \} , \quad C_1 = \{ 0, \alpha \}, \quad C_2 = \{ 0, \alpha , 2 \alpha\}, \ldots $$ En fait, on va montrer par récurrence que, pour tout $ n$, on a $C_n \subset C^*$, avec $$ C^* := \left\{ k \pi, \, 0 \le k < \lceil 2 \pi / \alpha \rceil \right\} \cup \left\{ 2 \pi - k \pi, \, 0 \le k < \lceil 2 \pi / \alpha \rceil \right\}. $$ L'ensemble $ C^*$ contient tous les $ k \alpha$ avec $ k \in \mathbb{N}$ tel que $ 0 \le k \alpha \le 2 \pi$, et tous les $ 2 \pi - k \alpha$ avec $ k \in \mathbb{N}$ tel que $ 0 \le k \alpha \le 2 \pi$. En particulier, il y aura au maximum $ \#(C^*) = 2 \lceil 2 \pi / \alpha \rceil$ coupes. Si $ p \in [0, 2 \pi]$ est une coupe à l'étape $ n$, cette coupe se trouve en $ p + \alpha$ après avoir tourné le gâteau. Deux cas se présentent : si $ p + \alpha < 2 \pi$, cette coupe n'ai pas dans la part qui va être retournée. En revanche, si $ p + \alpha > 2 \pi$, elle va être retournée. Le dessin suivant montre qu'après retournement, cette coupe se trouvera en $ \alpha - ( p + \alpha - 2 \pi) = 2 \pi - p$. 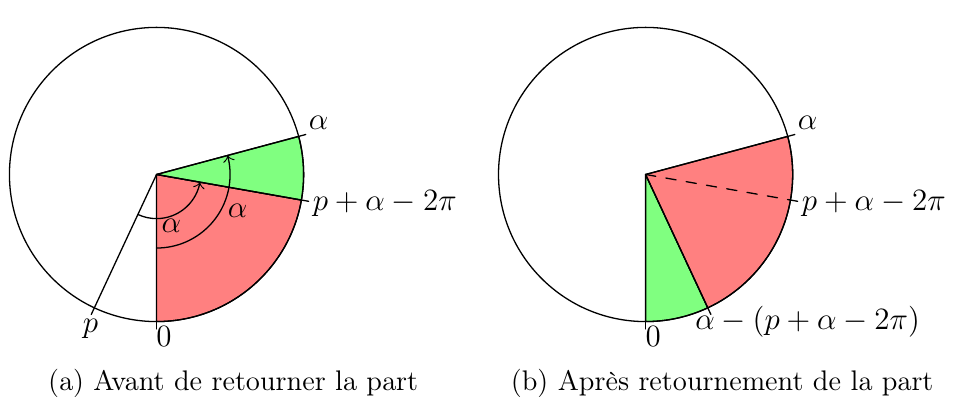RetournementPartGateau

On en déduit que $ C_{n+1} = f(C_n) \cup \{0\}$, où $ f$ est définie par $$ f(p) = \begin{cases} p + \alpha \quad \text{si} \quad p + \alpha < 2 \pi \\ 2 \pi - p \quad \text{sinon}. \end{cases} $$ On a donc $ C_{n+1} = f(C_n) \cup \{0\}$. Par ailleurs, on a $ C^* = f(C^*)$ et $ C_0 \subset C^*$. On en déduit par récurrence que $ C_n \subset C^*$ pour tout $ n \in \mathbb{N}$. Ainsi, quitte à rajouter des coupes fictives, on peut supposer que $ C_n = C^*$. L'ensemble de toutes les configurations de couleurs des parts de $ C^*$ est fini. Lorsque qu'on itère les étapes, on parcourt donc un cycle dans cet ensemble de configurations. Comme $ C_0$ (qui correspond à la configuration où le gâteau est entièrement blanc dessus) est dans ce cycle, et que le trajet est réversible (dans le sens où on peut retrouver les étapes précédentes), on repasse par $ C_0$ en un nombre fini d'étapes, ce qu'il fallait démontrer.

En plus simple, voici un problème qu'on m'a posé dans un stage de mathématiques.

Le minotaure (*)
Dans la ville de Cnossos se trouve un labyrinthe qui a la particularité suivante : de chaque salle de ce labyrinthe part trois couloirs. Le roi Minos y place dans un Minotaure, qui effectue inlassablement la routine suivante : il marche dans un couloir, tombe sur une salle, et prend une fois sur deux le couloir de droite, et une fois sur deux le couloir de gauche. Montrer que le Minotaure reviendra à son point initial.

Cette fois, on prend comme ensemble des configurations l'ensemble des couples $ (s_1, s_2, d)$, où $ s_1$ indique la salle d'où vient le minotaure, $ s_2$ la salle où il est, et $ d$ est la direction qu'il doit prendre (droite ou gauche). Cet ensemble de configurations est fini, donc le minotaure effectue un cycle dans cet ensemble. De plus, on peut deviner le passé du trajet du minotaure en connaissant n'importe quel point de ce cycle, donc tout son passé se trouve dans ce cycle. En particulier, le minotaure revient dans la salle initiale.