La réponse est oui, et voici la solution pour mettre 337 biscuits dans une boite de taille 4x336.
L'idée est de mettre les biscuits 6 par 6, en répétant la configuration suivante :
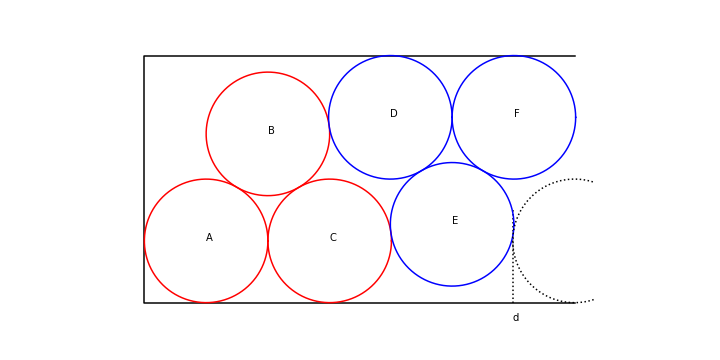
En effet, tentons de calculer d sur la figure. On note \((x_A, y_A)\) les coordonnées du centre du disque \(A\), etc. On trouve directement
$$
(x_A, y_A)= (1, 1) \quad \text{et} \quad (x_C, y_C)= (3,1).
$$
De plus, comme les centres des cercles \(A, B, C\) forment un triangle équilatéral, on trouve
$$
(x_B,y_B) = (2, 1 + \sqrt{3}).
$$
On a aussi : \(y_D = 3\). Le nombre \(x_D\) est plus complexe à trouver. En écrivant que la distance \(BD\) est \(2\), on obtient le système
$$
\begin{cases} (x_B - x_D)^2 + (y_B - y_D)^2 = 4 \\ y_D = 3 \end{cases}
$$
ce qui donne \(x_D^2 - 4x_D + 7 - 4 \sqrt{3} = 0\), et donc \(x_D = 2 + \sqrt{4 \sqrt{3} - 3}\). En répétant ces calculs, on déduit que \(d = 2 (x_D - 1)\), et enfin \(d = 2+2\sqrt{4 \sqrt{3} - 3} \approx 5.963939\).
On remarque que \(d < 6\), on a donc réussi à placer 6 biscuits sur une distance strictement plus petite que 6. Si on répète l'opération 56 fois, on place 56x6 = 336 biscuits dans une boite de longueur \(1 + 66 \times d \approx 334.98 < 335\) (le 1 vient du fait que le dernier biscuit \(F\) dépasse au dessus), et, en rajoutant un biscuit dans le coin en bas à droite, on place \(337\) biscuits dans une boite de taille \(336\).
