I am associate professor ("maître de conférences") at Ceremade, the mathematics department of Université Paris-Dauphine. I am a member of the research group "Probability and Statistics".
Contact
- E-mail: last_name @ ceremade.dauphine.fr
- Address: Université Paris-Dauphine, Place du Maréchal de Lattre de Tassigny, 75 775 Paris Cedex 16, France.
Teaching
The teaching material is available on Teams.Research
My research work deals with several discrete probability models originating from statistical mechanics, such as activated random walks, sandpile models, spin models or percolation.
I completed my PhD at ENS Paris, under the supervision of Raphaël Cerf, about self-organized criticality. Then, I was a temporary teaching and research assistant ("attaché temporaire d'enseignement et de recherche") at Aix-Marseille Université, where I worked on activated random walks with Alexandre Gaudillière and Amine Asselah. After this, I was a postdoc student in the university "La Sapienza" in Rome, where I studied models of interacting random loops, spin models and sanpile models, with Lorenzo Taggi, Matteo Quattropani, Alexandra Quitmann and Concetta Campailla.
Self-Organized Criticality
The concept of self-organized criticality aims at describing some physical systems which present a “critical” behaviour without having to tune a parameter like temperature to a critical value.
During my PhD thesis with Raphaël Cerf, we defined several toy models presenting this phenomenon, building upon percolation and the Ising model. More precisely, our construction relies on the introduction of a feedback mechanism which forces the system towards a critical regime.
|
Link to my PhD dissertation (in French):
|
|
Some toy models of self-organized criticality in percolation
ALEA, Lat. Am. J. Probab. Math. Stat. 19 (2022), 367–416 |
|
|
A planar Ising model of self-organized criticality Probab. Theory Related Fields 180 (2021), 163-198 |
|
An extension of the Ising-Curie-Weiss model of self-organized criticality with a threshold on the interaction range Electron. J. Probab. 29 (2024), article no. 15, 1–27. |
|
Activated Random Walks
Activated Random Walks is a system of interacting particles in which particles perform random walks on a graph, falling asleep at a certain rate and being waken up when another particle arrives on the same site. There is a phase transition, with a critical density separating a stable phase where particles eventually fall asleep for good and an active phase where activity is maintained indefinitely. This model can be seen as a stochastic variant of the abelian sandpile model, which was put forward to illustrate the concept of self-organized criticality.
With Alexandre Gaudillière and Amine Asselah, we showed that in dimension 2 the critical density is strictly below 1, concluding a series of works aimed at demonstrating the non-triviality of the phase transition in any dimension.
|
Active Phase for Activated Random Walks on the Lattice in all Dimensions
Ann. Inst. Henri Poincaré Probab. Stat. 60 (2024), no. 2, 1188–1214 |
|
The Critical Density for Activated Random Walks is always less than 1
Ann. Probab. 52(5): 1607-1649 (September 2024) |
|
I also got interested in the density conjecture, which connects several different definitions of the critical density of the model. In the direction of this conjecture I obtained a partial result in dimension 1:
|
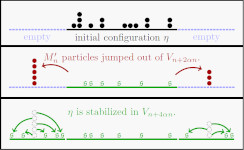
Macroscopic flow out of a segment for Activated Random Walks in dimension 1
To appear in ALEA, Lat. Am. J. Probab. Math. Stat. (2025) |
Still in dimension 1, this conjecture was proved by Christopher Hoffman, Tobias Johnson and Matthew Junge. In the following note, I present an alternative approach inspired by their superadditivity argument:
|
A new proof of superadditivity and of the density conjecture for Activated Random Walks on the line Preprint (2025) |
|
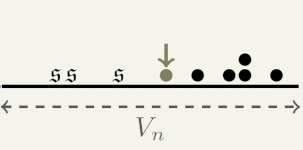
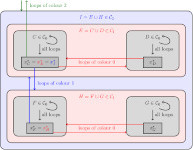
Stochastic Sandpile Model
With Concetta Campailla and Lorenzo Taggi, we are interested in the stochastic sandpile model, which can be seen as an intermediate between activated random walks and the abelian sandpile. In particular, we show in the following article that the critical density of this model is strictly less than 1 in any dimension:
|
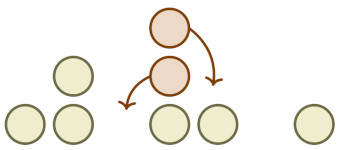
The critical density of the Stochastic Sandpile Model
Preprint (2024) |
Interacting random loops
With Lorenzo Taggi, Matteo Quattropani and Alexandra Quitmann, I studied models of interacting random loops which are connected with several models of interest in statistical mechanics, such as the spin O(n) model, the Bose gas or the double dimer model.
We got interested in various questions relating to this family of models, in particular the existence of macroscopic loops, i.e., of a length proportional to the size of the graph when the latter tends towards infinity.
|
Coexistence, enhancements and short loops in random walk loop soups
Probab. Math. Phys. 5 (2024), no. 3, 753–784 |
|