Je suis maître de conférences en probabilités au Ceremade, le laboratoire de mathématiques de l'Université Paris-Dauphine.

Contact
- E-mail : nom @ ceremade . dauphine . fr
- Adresse : Université Paris-Dauphine, Place du Maréchal de Lattre de Tassigny, 75 775 Paris Cedex 16.
Enseignement
Contrôle des chaînes de Markov (M1)
Les documents liés au cours sont disponibles sur Teams.Prérentrée de probabilités (M2 MATH)
 Notes de cours (merci de me signaler si vous voyez des coquilles)
Notes de cours (merci de me signaler si vous voyez des coquilles)
Recherche
Mon travail de recherche porte sur des modèles de probabilités discrètes en lien avec la mécanique statistique :
- Marches aléatoires activées
- Tas de sable stochastique
- Criticité auto-organisée
- Boucles aléatoires en interaction
Marches aléatoires activées
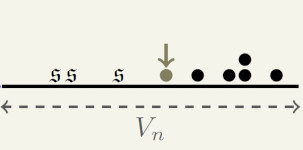
Le modèle des marches aléatoires activées est un système de particules en interaction dans lequel les particules effectuent des marches aléatoires sur un graphe en s'endormant à un certain taux et se réveillent quand une autre particule arrive sur le même site.
Ce modèle a émergé comme une variante de modèles de tas de sable, qui avaient été proposés par des physiciens pour illustrer le concept de criticité auto-organisée.
Il y a une transition de phase : une densité critique sépare une phase stable (où les particules s'endorment pour de bon) et une phase active (où l'activité se maintient).
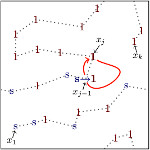
Avec Alexandre Gaudillière et Amine Asselah, nous avons montré qu'en dimension 2 la densité critique est strictement inférieure à 1, concluant ainsi une série de travaux visant à montrer la non-trivialité de la transition de phase en toute dimension.
|
Active Phase for Activated Random Walks on the Lattice in all Dimensions
Ann. Inst. Henri Poincaré Probab. Stat. 60 (2024), no. 2, 1188–1214 |
Alors que l'article ci-dessus porte sur le cas où le taux d'endormissement est petit, la publication suivante traite le cas plus général :
|
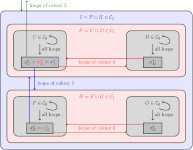
The Critical Density for Activated Random Walks is always less than 1
Ann. Probab. 52(5): 1607-1649 (September 2024) |
|
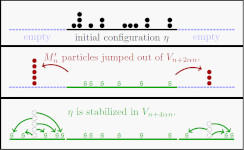
Le travail suivant montre que la stabilisation d'un segment contenant une densité surcritique fait sortir une fraction des particules par les bords du segment. On peut voir cela comme un premier pas vers la conjecture de la densité, qui relie différentes définitions de la densité critique du modèle.
|
Macroscopic flow out of a segment for Activated Random Walks in dimension 1
ALEA, Lat. Am. J. Probab. Math. Stat. 22, 557-577 (2025) |
Cette conjecture de la densité a été démontrée en dimension 1 par Christopher Hoffman, Tobias Johnson et Matthew Junge. L'article suivant présente une nouvelle preuve de ce résultat, basée sur une propriété de superadditivité pour la densité stationnaire du modèle (alors que le travail de Hoffman, Johnson et Junge repose sur la superadditivité d'une quantité différente, qui est indirectement reliée à la densité stationnaire).
|
A new proof of superadditivity and of the density conjecture for Activated Random Walks on the line Prépublication (2025) |
|
Avec Christopher Hoffman, Tobias Johnson, Josh Meisel, Jacob Richey et Leonardo Rolla, nous avons étendu un résultat de Madeline Brown, Christopher Hoffman et Hyojeong Son sur l'explosivité du modèle en dimension 1 : partant d'une configuration surcritique, une seule particule active suffit pour réveiller toutes les autres avec probabilité positive.
|
Explosivity in 1-d Activated Random Walk
Prépublication (2026) |
Tas de sable stochastique
Le tas de sable stochastique est un modèle proche, qui peut être vu comme un intermédiaire entre les marches aléatoires activées et le tas de sable abélien, le modèle initialement proposé par les physiciens qui a lancé cette ligne de recherche.
Avec Concetta Campailla et Lorenzo Taggi, nous avons montré que la densité critique de ce modèle est strictement inférieure à 1 en toute dimension :
|
The critical density of the Stochastic Sandpile Model
Prépublication (2024) |
|
L'article suivant explique comment échantillonner la mesure stationnaire de ce modèle sur n'importe quel graphe, et étudie le cas du graphe complet :
|
Stochastic Sandpile model: exact sampling and complete graph
à paraître dans Electron. J. Probab. (2025) |
Criticité auto-organisée
Le concept de criticité auto-organisée vise à décrire certains systèmes physiques qui présentent un comportement « critique » sans qu'il y ait besoin d'ajuster précisément un paramètre (comme la température) à une valeur critique. C'est l'une des motivations pour étudier les modèles de tas de sable et de marches aléatoires activées.
Avec Raphaël Cerf (qui a encadré ma thèse), nous avons construit plusieurs modèles-jouets qui présentent ce phénomène, à partir de la percolation et du modèle d'Ising. Notre construction repose sur l'introduction d'un mécanisme de rétroaction qui force le système à fonctionner au voisinage d'un point critique.

|
Le manuscrit de ma thèse :
|
Les deux articles suivants présentent des variantes « auto-critiques » de la percolation et du modèle d'Ising:
|
Some toy models of self-organized criticality in percolation
ALEA, Lat. Am. J. Probab. Math. Stat. 19 (2022), 367–416 |
|

|
A planar Ising model of self-organized criticality Probab. Theory Related Fields 180 (2021), 163-198 |
Le travail suivant considère un modèle de criticité auto-organisée construit par Matthias Gorny, et étudie ce qui se passe si l'interaction de type champ moyen est remplacée par des interactions à longue portée :
|
An extension of the Ising-Curie-Weiss model of self-organized criticality with a threshold on the interaction range Electron. J. Probab. 29 (2024), article no. 15, 1–27. |
|
Boucles aléatoires en interaction
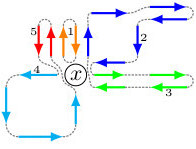
L'article suivant, écrit avec Lorenzo Taggi, Matteo Quattropani et Alexandra Quitmann, porte sur des modèles de boucles aléatoires en interaction qui sont reliés à différents modèles de mécanique statistique, dont le modèle Spin O(n), le gaz de Bose ou encore le modèle des doubles dimères.
|
Coexistence, enhancements and short loops in random walk loop soups
Probab. Math. Phys. 5 (2024), no. 3, 753–784 |