Exercices d'Analyse complexe

Soit \(D \subsetneq \C\) un ouvert.

• Soit \(N \in \N \cup \{\infty\}\) le nombre de composantes connexes de \(D\) (les composantes connexes sont les parties connexes maximales pour l'inclusion). En particulier, si \(N=0\) ou \(1\), \(D\) est connexe.
  
• Soit aussi \(M \in \N_* \cup \{\infty\}\) le nombre de composantes connexes du complémentaire \(\C \setminus D\). \(M\) s'appelle l'ordre de connexité de \(D\). Dans le cas où \(D\) est connexe (sinon, \(M\) est moins utilisé),
  
  • si \(M=1\), \(D\) est simplement connexe ;
    
  • si \(M=2\), \(D\) est doublement connexe ;
    
  • … ;
    
  • si \(M==\infty\), \(D\) est infiniement connexe.
    

On considère maintenant les trois ouverts hachurés ci-dessous.

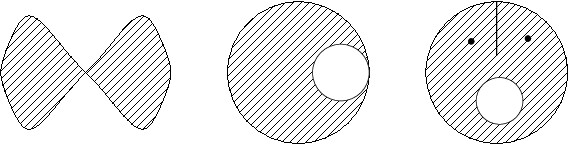
1. Sont-ils connexes?
   
2. Pour ceux qui ne sont pas connexes, quel est le nombre \(N\) de leurs composantes connexes ?
   
3. Pour ceux qui sont connexes, quel est leur ordre de connexité \(M\) ?
   

1. Expliciter l'application injective \( j : M_1(\C) \equiv \C \hookrightarrow M_2(\R)\) induite de l'application injective \(L_\C(\C) \hookrightarrow L_\R(\C)\).
   

Soit \(f = u+iv : \C \to \C\) une fonction \(\R\)-dérivable. Elle est \(\C\)-dérivable si sa différentielle
\[df = \begin{pmatrix} \partial_x u &\partial_y u\\ \partial_x v &\partial_y v \end{pmatrix}\]
est \(\C\)-linéaire, c'est-à-dire dans l'image de l'application \(j\).

2. Retrouver les équations de Cauchy-Riemann qui caractérisent les fonctions \(\C\)-dérivables.
   

Dans un espace métrique, une similitude est une transformation \(s\) de l'espace qui multiplie toutes les distances par une constante \(r \in \R\) :
\[d(s(x),s(y)) = r \, d(x,y);\]
\(r\) s'appelle le rapport de similarité.

Soit \(s\) une similitude d'un espace euclidien \(E\).

1. Montrer que \(s\) est une application affine, i.e. que l'application \(\sigma : z \mapsto s(z) - s(0)\) est linéaire. On pourra commencer par montrer que \(\sigma\) multiplie le produit scalaire par \(r^2\).
   

On suppose dorénavant que \(E = \C = \R^2\).

2. Montrer qu'une similitude est de la forme \(s(z) = az + d\) (similitude directe) ou \(s(z) = a\bar z + d\) (similitude indirecte).
   
3. Pour ceux qui connaissent ces concepts: Montrer que le sous-groupe des similitudes directes (i.e. telles que le déterminant de leur partie linéaire est \(>0\)) et le sous-groupe des isométries affines (déplacements) sont distingués.
   

Soient \(D\subset \C\) une droite réelle (c'est à dire un sous-espace vectoriel réel de dimension un), et \(s\) la symétrie orthogonale par rapport à cette droite. Montrer (sans trop de calcul) qu'il existe un nombre complexe \(\lambda\), de module \(1\), tel que \(s(z)=\lambda \bar z\). Relier l'argument de \(\lambda\) à l'angle entre la droite \(D\) et l'axe réel.

1. Exprimer l'application linéaire de matrice \(\begin{bmatrix} 1&1\\0&1\end{bmatrix}\) sous la forme \(ℓ(z)=\lambda z+\mu \bar z\).
   

Soient \(E\) et \(F\) des \(\C\)-espace vectoriel. On note \(L_{\R}(E,F)\), \(L_{\C}(E,F)\) et \(L_{\bar \C}(E,F)\) les espaces d'applications de \(E\) dans \(F\) respectivement \(\R\)-linéaires, \(\C\)-linéaires et \(\C\)-antilinéaires, c'est-à-dire telles que \(ℓ(\lambda z+\mu w)=\bar \lambda \ell(z)+\bar \mu \ell(w)\) pour tout \(\lambda , \mu\in \C\), \(z,w\in E\).

2. \(L_{\R}(E,F)\), \(L_{\C}(E,F)\), \(L_{\bar \C}(E,F)\) sont-ils des \(\R\)-espaces vectoriels? Des \(\C\)-espaces vectoriels?
   
3. Quelles inclusions y a-t-il entre ces trois espaces?
   
4. Déterminer \(L_{\bar \C}(E,F)\cap L_{\C}(E,F)\).
   
5. Pour tout \(\ell\in L_{\R}(E,F)\), montrer que \(\ell(z)-i\ell(iz)\) est \(\C\)-linéaire.
   
6. Montrer que \(L_{\R}(E,F)=L_{\C}(E,F)\oplus L_{\bar \C}(E,F)\).
   
7. Dans le cas où \(E=F=\C\), décrire géométriquement et algébriquement \(L_\C(\C)\) et \(L_{\bar \C}(\C)\).
   

Le corps (associatif mais non commutatif) \(\H\) des quaternions est la structure de corps de \(\R^4\) obtenue avec la structure vectorielle standard de \(\R^4\) et la multiplication induite par le fait que, si l'on note \((1,i,j,k)\) la base canonique de \(\R^4\), \(1\) est l'élément neutre, et \[ij = k, \quad jk = i,\quad ki=j, \quad i^2=j^2=k^2=-1.\]

L'opération de conjugaison des quaternions est
\[q= \alpha + \beta i + \gamma j + \delta k \longmapsto \bar q= \alpha - \beta i - \gamma j - \delta k~;\] comme avec les complexes, la norme euclidienne de \(q\) est telle que \(\|q\|^2 = q \bar q\) ; mais attention au fait que \(\overline{pq} = \overline{q} \, \overline{p}\). La partie réelle de \(q\) est \(\alpha\) et sa partie imaginaire est \(q-\alpha\).

1. Vérifier que tout élément non nul est \(\H\) est inversible (ce qui fait que \(\H\) n'est pas seulement une algèbre, mais un corps).
   

Nous noterons \(\Sb\) la sphère unité de \(\H\) et \(\Im \H\) l'hyperplan vectoriel de \(\H\) des quaternions de partie réelle nulle.

2. Montrer que \(\Sb\) est un sous-groupe multiplicatif donc \(\Sb\) est stable par multiplication.
   

Notons
\[\rho : \begin{array}[t]{lll} \Sb &\rightarrow &\mathrm{Gl}(\Im \H)\\ q &\mapsto & \rho_q, \quad \rho_q : x \mapsto qxq^{-1} = qx \bar q. \end{array} \]
Cette application s'appelle la représentation adjointe du groupe \(\Sb\) dans \(\Im \H\). (Une représentation de groupe permet d'étudier un groupe par la façon dont il "agit" sur un espace vectoriel, ou sur un autre ensemble.)

3. Montrer que cette application est bien définie.
   
4. Montrer que \(\rho\) est à valeurs dans \(SO(\Im\H) \equiv SO_3\). On pourra donc noter \(\rho : \Sb \rightarrow SO_3\).
   
5. Décrire la roation \(\rho_q\) en fonction de \(q\).
   
6. Montrer que l'application \(\rho\) est surjective de degré de surjectivité \(2\).
   

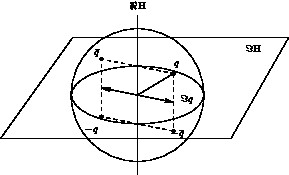
Considérons la relation d'équivalence de l'antipodie sur \(\Sb\), pour laquelle \(q \sim -q\). L'espace topologique quotient de
\(\Sb\) par \(\sim\) est, par définition l'espace projectif \(\R\Pb^3\).

7. Montrer que \(\rho\) induit un homéomorphisme \(\tilde\rho : \R\Pb^3 \rightarrow SO_3\).
   

On peut déduire de cette construction que \(SO_3\) n'est pas simplement connexe et que son revêtement universel est de degré \(2\).

Soit \(*\) le produit sur \(\C\) défini par
\[z₁ * z₂ = (x₁x₂ + y₁y₂) + i (x₁y₂ + x₂y₁) \quad (z_j = x_j+iy_j), \; j=1,2\]
(donc \(i*i=1\), au lieu de \(i² =-1\)).

1. Montrer que ce produit prolonge celui de \(\R\) et que \((\C,+,*)\) est une \(\R\)-algèbre associative commutative.
   

   (On rappelle que, si \(K\) est un corps commutatif, une \(K\)-algèbre associative commutative est un \(K\)-espace vectoriel \(A\) muni d'une loi de multiplication \(* : A^2 \to A\) telle que
   

   • \((a+b)*c = a*c + b*c\) (distributivité à gauche)
     
   • \(a*(b+c)=a*b+a*c\) (distributivité à droite)
     
   • \((\alpha a)*(\beta b) = (\alpha\beta) (ab)\)
     
   • \(a*(b*c) = (a*b)*c\) (associativité)
     
   • \(a*b=b*a\) (commutativité).)
     

On définit le module de \(z\) comme \(\|z\| = \sqrt{|z*\bar z|}\).

2. Trouver le lieu géométrique des points \(z\) de module unité. Montrer que \(\|z_1 z_2\| = \|z_1\| \, \|z_2\|\) et que \(\|z\|=0\) si et seulement si \(z\) est diviseur de zéro.
   

Si \(z_2 \neq 0\), on définit le quotient par \(z_2\) avec la formule
\[z_1 / z_2 = \frac{z_1 * \bar z_2}{z_2 * \bar z_2}.\]

3. Montrer que
   \[(z_1 / z_2) * z_2 = z_1.\]
   

Si \(f\) est une fonction définie localement au voisinage de \(z\), la dérivée hyperbolique de \(f\) en \(z\) est la limite, si elle existe,
\[f'(z) = \lim_{h \to 0, \quad \|h\| \neq 0} \frac{f(z+h)-f(z)}{h}.\]

4. Montrer que cette limite existe si et seulement si, en notant \(f = u+iv\),
   \[\partial_x u = \partial_y v, \quad \partial_y u = \partial_x v.\]
   

On définit \(e_*^z\) par la même série que pour l'exponentielle ordinaire, mais en remplaçant les puissances de \(z\) relatives au produit habituel par les puissances relatives au produit modifié.

5. Comparer cette fonction à l'exponentielle ordinaire.
   

Remarque : Un théorème célèbre de Frobenius, démontré en 1877, caractérise les extensions de corps de dimension finie du corps commutatif \(\R\) des réels. Il n'y en a que deux (à isomorphisme près) : le corps \(\C\) des complexes et le corps \(\H\) des quaternions. Parmi ces deux extensions, seule la première est commutative.

Soit \(P\) un polynôme complexe. Montrer que les racines de \(P'\) sont dans l'enveloppe convexe des racines de \(P\).

On définit le plan compactifié \(\hat\C\) comme \(\hat\C = \C \cup \{\infty\}\), où \(\infty\) est le symbole d'un point (appelé infini) ajouté au plan complexe.

Nous allons identifier \(\hat \C\) à la sphère \(\Sb^2 = \{(X,Y,Z) \in \R^3, \, X^2+Y^2+Z^2 =1\}\).

Soit \(\pi : \C \to \Sb^2\), \(z = x + iy \mapsto W = (X,Y,Z)\) la projection stéréographique qui, à tout point \(z \in \C\), associe le point d'intersection de la sphère \(\Sb^2\) avec le rayon qui joint le pôle Nord \(N = (0,0,1)\) au point \(z\).

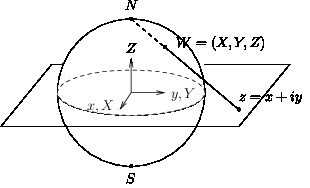
1. Où sont envoyés par \(\pi\) le disque (ouvert) \(D(0,1) = \{|z|<1\}\), son extérieur ouvert \(E(0,1) = \{|z|>1\}\) et le cercle \(C(0,1)\) ?
   
2. Montrer que
   \[X + iY = \frac{2z}{1+|z|^2}, \quad Z = \frac{|z|^2-1}{|z|^2+1}\]
   et que, inversement,
   \[z = \frac{X+iY}{1-Z}.\]
   
3. Quelle est la limite de \(\pi(z)\) quand \(|z| \to \infty\)?
   

On prolonge \(\pi\) "par continuité" (on n'a pas encore défini de topologie sur \(\hat\C\)) en posant \(\pi(\infty) = N\).

4. Montrer que ce prolongement est une bijection \(\pi : \hat\C \to \Sb^2\), qui permet d'identifier \(\hat\C\) et \(\Sb^2\).
   

Définissons sur \(\hat\C\) la distance \(d\) héritée de la distance euclidienne sur \(\Sb^2\), de sorte que l'application \(\pi\) est ainsi une isométrie (et donc un homéomorphisme et même un lipéomorphisme).

5. Montrer que
   \[d(z,w) = \frac{2|z-w|}{\sqrt{1+|z|^2}\sqrt{1+|w|^2}} \quad (\forall z,w \in \C) \quad \mbox{et que} \quad d(z,\infty) = \frac{2}{\sqrt{1+|z|^2}} \quad (\forall z \in \C).\]
   
6. Montrer que la restriction de \(d\) à \(\C\) est équivalente à la métrique euclidienne, puisque, sur \(D(0,R) = \{|z| \leq R \}\) (\(R < \infty\)),
   \[\frac{2|z-w|}{1+R^2} \leq d(z,w) \le 2 |z-w|.\]
   
7. Par exemple, quels sont les points d'accumulation de \(\Z\) dans \(\hat\C\)?
   
8. Montrer que l'espace métrique \((\hat \C,d)\) est compact.
   

Le corollaire immédiat est que \((\hat \C,d)\) est séquentiellement compact (toute suite de \(\hat\C\) possède une valeur d'adhérence, d'après le théorème de Bolzano-Weierstrass), et complet (toute suite de Cauchy possède une valeur d'adhérence donc converge).

1. Soit \(z_n=x_n+i y_n\) une suite de nombres complexes. Montrer que \(|z_n| \to 0\) si et seulement si \(|x_n|+|y_n|\to 0\).
   
2. Soit \(f:\C\to \C\) une fonction. Montrer l'équivalence entre
   
   1. \(f(z)=|z|\epsilon(z)\), où \(\epsilon\) tend vers \(0\) en \(0\).
      
   2. \(f(x+iy)=(|x|+|y|) \epsilon (x+iy)\) où \(\epsilon\) tend vers \(0\) en \(0\).
      
   3. \(f(z)=z\epsilon (z)\) ou \(\epsilon\) tend vers \(0\) en \(0\).
      

Dans ces cas, on écrit \(f(z) = o(z)\).

Lesquelles des deux fonctions suivantes sont \(\C\)-dérivables :
\[f(x+iy)=x^2-y^2+2ixy, \quad g(x+iy)=x^2+y^2-2ixy \quad ?\]

Soient \(D\) un domaine de \(\C\), \(a \in D\) et \(f : D \to \C\) une fonction dérivable en \(z\) ; sa différentielle en \(z\) est une application \(\R\)-linéaire, donc de la forme
\[df(z) = a \, dz + b \, d\bar z,\]
avec \(a,b \in \C\).

1. Calculer la variation \(\Delta f\) de \(f\) entre \(z\) et \(z+\Delta z\), avec \(\Delta z = \Delta r \, e^{i\theta}\), au premier ordre en \(\Delta r\), en fonction de \(a\) et \(b\).
   
2. En déduire, quand \(\theta\) est fixé, la valeur de
   \[\partial_{z_\theta} f (z) := \lim_{\Delta r \to 0} \frac{\Delta f}{\Delta z}\]
   en fonction de \(a\) et \(b\).
   
3. Conclure que \(f\) est \(\C\)-dérivable en \(a\) si et seulement si \(\partial_{z_\theta}f(a)\) ne dépend pas de \(\theta\).
   

Soient \(n\in\Z\) et \(f(z)=z^n\).

1. Montrer que, si \(n \geq 1\), \(f\) est holomorphe sur \(\C\) et que \(f'(z) = n z^{n-1}\).
   
2. Montrer que, si \(n\leq -1\) est un entier négatif, \(f\) est holomorphe sur \(\C\backslash\{0\}\) et que la formule pour la dérivée reste valide.
   

1. Retrouver la définition des opérateurs \(\partial_z = \frac{\partial}{\partial z}\) (« del z ») et \(\partial_{\bar z} = \frac{\partial}{\partial \bar z}\) (« del z barre »), tels que
   

   \begin{align*} df &= \partial_x f \, dx + \partial_y f \, dy\\ & = \partial_z f \, dz + \partial_{\bar z} f \, d\bar z \end{align*}

   (autrement dit, ces opérateurs forment une sorte de base duale des formes linéaires \(dz = dx + i \, dy\) et \(d\bar z = dx - i dy\)).
   

2. Montrer que
   \[\partial_{\bar z} z= \partial_z \bar z = 0, \quad \partial_z z = \partial_{\bar z} \bar z = 1.\]
   
3. Traduire les équations (CR) en terme des deux nouveaux opérateurs.
   

On admettra ou démontrera que les deux opérateurs satisfont les règles habituelles de dérivation partielle par rapport à des variables indépendantes : si \(f\) et \(g\) sont de classe \(C^1\),
\[\partial_{z} (f+g) = \partial_z f + \partial_z g, \quad \partial_z(fg) = (\partial_z f)g + f (\partial_z g),\]
et de même avec \(\partial_{\bar z}\), ainsi que les règles de dérivation des fonctions composées. Par exemple, si \(f\) est holomorphe en \(z\) et \(g\) en \(f(z)\), \[(g ∘ f)'(z) = g'(f(z)) f'(z) ;\]
la démonstration est la même que dans le cas réel.

En particulier, pour une fonction \(f(z) = P(z,\bar z)\), où \(P\) un polynôme complexe de deux variables,
\[\partial_z f(z)=\partial_1 P(z,\bar z) \quad \mbox{et} \quad \partial_{\bar z} f( z)=\partial_2 P(z,\bar z)\]
(où \(\partial_j P\) est la dérivée partielle de \(P\) par rapport à la \(j\)-ième variable.

4. Calculer les dérivées \(\partial_z f\) et \(\partial_{\bar z} f\) pour \(f(z)=z^2-i\bar z\).
   

On rappelle que les équations de Cauchy-Riemann (CR), qui caractérisent les fonctions holomorphes \(f = u+iv\), sont
\[\partial_x u = \partial_y v, \quad \partial_x v = - \partial_y u.\]

5. Montrer qu'une séries entières convergente \(f(z) = \sum_{p,q \geq 0} f_{p,q} z^p \bar z^q\) est holomorphe si et seulement si \(f_{p,q} = 0\) dès que \(q \neq 0\).
   

On verra ultérieurement que les fonctions holomorphes sont analytiques (i.e. localement développables en séries entières de \(z\)). Donc elles peuvent être considérées comme des fonctions holomorphes de \(z\) « indépendantes » de \(\bar z\) (sachant que \(\bar z\) est bien sûr une fonction de \(z\), mais pas une fonction holomorphe). Pour cette raison, les fonctions de \(z\) s'écrivent parfois \(f(z,\bar z)\), et l'on réserve la notation \(f(z)\) aux fonctions holomorphes.

Une application homographique est une fonction de la forme
\[h : \C \setminus \{-\frac{d}{c} \} \to \C, \quad z \mapsto \frac{az+b}{cz+d}, \quad a,b,c,d \in \C, \quad ad-bc \neq 0\]
(avec \(-\frac{d}{c} = ∞\) si \(c=0\)). La condition \(ad-bc \neq 0\) exclut le cas constant puisque la fraction rationnelle est alors irréductible.

Pour \(c=0\) on a forcément \(ad \neq 0\) et l'application est affine :
\[h(x) = \frac{a}{d} z + \frac{b}{d} = A z +B\]
avec \(A \neq 0\). L'application est donc la composée de la translation \(z \mapsto z + B/A\) et de la similitude \(z \mapsto Az\), et se prolonge sur \(\hat\C\) en posant \(h(∞) = ∞\).

Pour \(c ≠ 0\), la fonction est définie initialement en dehors de \(z=-d/C\) et \(z=∞\). On la prolonge en une application \(\hat\C \to \hat\C\) en posant
\[h \left( -\frac{d}{c} \right) = \infty \quad \mbox{et} \quad h(\infty) = \frac{a}{c}.\]

1. Montrer que \(h\) ainsi prolongée est un homéomorphisme \(\hat\C \to \hat\C\).
   
2. Montrer que, sur \(\C \setminus \{-d/c\}\), \(h\) est \(\C\)-dérivable et n'a pas de point critique (point d'annulation de \(h'\)).
   
3. Montrer que \(h : \hat\C \to \hat\C\) est holomorphe (pour ramener l'infini en \(0\), on utilisera les applications \(z \mapsto 1/z\) et \(w \mapsto 1/w\)).
   
4. (*) Montrer que \(h\) induit une transformation de la droite projective complexe \(\C\Pb^1 = (\C \setminus \{0\}) / \R\).
   
5. Montrer que l'ensemble \(\Hc\) des applications homographiques est un groupe (non commutatif) pour la composition.
   
6. Quel est le sous-groupe des applications homographiques fixant l'infini?
   

On convient d'appeler un cercle de \(\hat\C\) tout cercle ou toute droite de \(\C\).

7. Montrer qu'une application \(h \in \Hc\) envoie un cercle de \(\hat\C\) sur un cercle de \(\hat\C\).
   

8. Montrer que, pour tout triplet de points distincts \(z_1, z_2, z_3 \in \C\) et tout triplet \(w_1, w_2, w_3 \in \C\) de points distincts, il existe une unique \(h \in \Hc\) tel que \(h(z_j)=w_j\), \(j=1,2,3\).
   
9. En déduire que tout couple de disques de \(\hat\C\) sont biholomorphiquement équivalents (au sens où il existe une homographie qui applique bijectivement l'un sur l'autre).
   
10. Montrer que le sous-groupe de \(\Hc\) des homographies envoyant le disque \(D = D(0,1)\) sur lui-même (biholomorphismes de \(\C\)) est l'ensemble des homographies de la forme
    \[f(z) = e^{i\theta} \, \frac{z-a}{1-\bar a z}, \quad a \in D, \, \theta \in \R.\]
    

Soient \(\Omega\) un ouvert de \(\C_* = \C \setminus \{0\}\) et \(\theta : \Omega \to \R\) une fonction continue. On dit que \(\theta\) est une détermination continue de l'argument sur \(\Omega\) si, pour tout \(z \in \Omega\), \(\theta(z)\) est un argument de \(z\), i.e. \(\exp(i \theta(z)) = \frac{z}{|z|}\).

Montrer que deux déterminations continues de l'argument sur un ouvert connexe diffèrent d'un multiple entier de \(2\pi\).

La détermination principale de l'argument sur \(\C \setminus \R^-\) est l'unique détermination continue de l'argument \(\Omega \to ]-\pi,\pi[\).

On considère une série entière complexe \(∑_{n \geq 0} c_n (z-a)^n\).

1. Supposons que les termes de la série sont bornés en un point \(z_0 \in \C\), i.e. il existe \(M >0\) tel que
   \[|c_n(z_0-a)^n| \leq M \quad (\mbox{pour tout } n \in \N).\]
   Montrer que cette série converge sur le disque ouvert \(D = D(a,|z_0-a|)\) et qu'elle converge absolument uniformément sur tout sous-ensemble \(B \Subset D\). (On rappelle que cette dernière notation signifie qu'il existe un compact \(K\) tel que \(B \subset K \subset D\). Comme ici \(D\) est borné, cela est équivalent au fait que l'adhérence de \(B\) est incluse dans \(D\), puisqu'alors on peut prendre l'adhérence de \(B\) pour \(K\).)
   
2. Supposons que la série entière converge en un point \(z_0 \in \C\). Montrer qu'elle converge sur \(D = D(a,|z_0-a|)\) et qu'elle converge absolument uniformément sur tout compact \(K \subset D\).
   

Le rayon de convergence est
\[R = \sup \{ |\zeta| \; : \; \zeta \in \C, \; \sum_{n \geq 0} c_n \zeta^n \quad \mbox{converge simplement}\}.\]
D'après ce qui précède,
\[R = \sup \{ r \geq 0 \; : \; (c_n r^n)_{n \geq 0} \quad \mbox{bornée}\}.\]

3. Montrer que
   \[\frac{1}{R} = \limsup_{n \to +\infty} |a_n|^{1/n}.\]
   

Calculer le rayon de convergence des séries entières suivantes :

4. \(\sum z^n/n!\)
   
5. \(\sum q^{n^2} z^n\) où \(q\) vérifie \(\vert q \vert <1\)
   
6. \(\sum n^p z^n\) où \(p\) est un entier non nul
   
7. \(\sum a_n z^n\) où \(a_n\) vérifie \(a_n = a^n\) si \(n\) est pair et \(a_n = b^n\) si \(n\) est impair et \(a,b\) sont deux nombres complexes non nuls.
   

Dans cet exercice, on part de zéro. Pour \(z = x+iy \in \C\) on définit la fonction exponentielle par
\[e^z = \sum_{n \geq 0} \frac{z^n}{n!}\]
(série entière dont on sait que le rayon de convergence est infini).

1. Montrer que la fonction ainsi définie sur \(\C\) est sa propre dérivée.
   
2. Montrer que l'exponentielle est un morphisme \((\C,+) \to (\C,\times)\):
   \[e^{z+w} = e^z \, \times e^w.\]
   

En particulier, \(e^z \, e^{-z} = 1\), donc \(e^z \neq 0\) pour tout \(z\), et
\[e^{x+iy} = e^x \, e^{iy}.\]
Donc l'étude de l'exponentielle complexe se ramène à celle des deux fonctions \(e^x\) et \(e^{iy}\) de la variable réelle.

Soient \(μ\) une mesure finie (éventuellement complexe) sur un espace mesurable \(X\), \(φ\) une fonction complexe mesurable sur \(X\), \(D\) un domaine de \(\C\) qui ne rencontre pas \(φ(X)\) et
\[f(z) = ∫_X \frac{dμ(x)}{φ(x)-z}.\]

Montrer que \(f\) est définie sur \(D\) et qu'elle y est développable en série entière.

1. Soit \(f: [-1,1] \to \R\) est une fonction de classe \(C^1\) telle que \(f(0) = 0\). Rappeler pourquoi il existe une fonction \(g\) continue sur \([-1,1]\) telle que \(f(x) = x g(x)\) (c'est-à-dire que la fonction \(\frac{f(x)}{x}\) est continue). On pourra utiliser la formule de Taylor avec reste intégral.
   
2. Supposons maintenant que \(f(z)=\sum _{n\geq 0} a_nz^n\) est une série entière convergente, et toujours s'annulant en \(0\). Montrer que \(f(z)=z g(z)\), où \(g\) est une série entière qui a le même rayon de convergence que \(f\).
   

Soient \(\sum_{n \geq 0} a_nz^n\) et \(\sum_{n \geq 0} b_n z^n\) deux séries entières de rayons de convergence respectifs \(r_1\) et \(r_2\). On note
\(c_n = \sum_{0 \leq k \leq n} a_k b_{n-k} \) pour tout \(n \geq 0\).

Montrer que

1. le rayon de convergence de la série \(\sum_{n \geq 0} c_n z^n\) est \(\geq \min(r_1, r_2)\) ;
   
2. pour \(|z| \leq \min(r_1, r_2)\),
   \[\left( \sum_{n \geq 0} a_nz^n \right) \left( \sum_{n \geq 0} b_n z^n \right) = \sum_{n \geq 0} c_nz^n.\]
   

Considérons l'équation différentielle
\[x'(t) = v(x(t),t),\]
où \(v\) est une série convergente au voisinage de \((0,0)\):
\[v(x,t) = \sum_{p,q \geq 0} v_{p,q} x^p t^q.\]
On suppose que
\[|v_{p,q} | \leq \frac{M}{r^{p+q}}.\]

1. Montrer que la série entière \(v\) converge sur un voisinage de \((0,0)\).
   

On veut montrer qu'il existe une unique série entière convergente
\[x(t) = \sum_{n \geq 1} x_n t^n\]
convergente satisfaisant l'équation différentielle.

2. Montrer que, s'il existe une telle solution, ses coefficients sont déterminés par des relations du type :
   \[(n+1) x_{n+1} = P_{n+1}(x_1,...,x_n;\{v_{p,q}\}),\]
   où \(P_{n+1}\) est un polynôme universel par rapport aux coefficients précédents \(x_1\), …, \(x_n\) et par rapport à un nombre fini de coefficients \(v_{p,q}\), dont les coefficients sont dans \(\N\). En déduire que
   \[x_n = Q_n(\{v_{p,q}\}),\]
   où les \(Q_n\) sont des polynômes à coefficients rationnels \(\geq 0\), dépendant d'un nombre fini de coefficients \(v_{p,q}\).
   

On dit qu'une série entière
\[V(x,t) = \sum_{p,q \geq 0} V_{p,q} x^p t^q\]
à coefficients \(V_{p,q} \geq 0\) est une série marjorante de \(v(x,t)\) si ses coefficients satisfont les inégalités
\[|v_{p,q}| \leq V_{p,q}.\]
Soit \(X(t) = \sum_{n \geq 1} X_n t^n\) l'unique solution formelle de l'équation
\[X't) = V(X(t),t).\]

3. Montrer que \(X\) est une série majorante de \(x:
   \[|x_n| \leq X_n.\]
   
4. Trouver \)X\) si
   \[V_{p,q} = \frac{M}{r^{p+q}}.\]
   
5. Conclure.
   

Montrer que \(f(z) = 1/z\) n'a pas de primitive sur \(D^*(0,2) = \{ 0 < |z| < 2 \}\).

Soient \(\emptyset \neq D \subset \hat\C\) un domaine et \(a \in D\). Soit \(\Lc_a\) l'ensemble des lacets \(\gamma : [0,1] \to D\) tels que \(\gamma(0) = \gamma(1) = a\). Si \(\gamma,\delta \in \Lc_a\), on définit leur concaténation \(\gamma * \delta \in \Lc_a\) telle que
\[\gamma * \delta (t) = \begin{cases} \gamma(2t) &\mbox{si } 0 \leq t \leq 1/2\\ \delta(2(t-1)) &\mbox{si } 1/2 \leq t \leq 1. \end{cases}\]

1. Montrer que l'opération de concaténation n'est pas une loi de groupe sur \(\Lc_a\).
   

Soit \(\pi_1(D,a)\) le quotient de \(\Lc_a\) par la relation d'homotopie.

2. Montrer que la concaténation induit une loi de groupe sur \(\pi_1(D,a)\).
   
3. Soit \(b \in D\). Montrer que \(\pi_1(D,a)\) et \(\pi_1(D,b)\) sont isomorphes.
   

Pour cette raison, \(\pi_1(D,a)\) se note abusivement \(\pi_1(D)\) est s'appelle le premier groupe d'homotopie de \(D\).

1. Montrer que \(\pi_1(D)\) est trivial si et seulement si toute paire de chemins de \(D\) d'extrémités communes sont homotopes dans \(D\).
   

Supposons que la frontière d'un domaine \(D\) borné est constituée d'un nombre fini de courbes fermées \(\gamma_0\), …, \(\gamma_n\). Admettons que la frontière extérieure \(\gamma_0\), c'est-à-dire la courbe séparant les points de \(D\) de l'infini, est orientée dans le sens direct, et les autres dans le sens rétrograde. (Autrement dit, les courbes sont orientées de sorte que le domaine reste toujours à gauche du sens de parcours.) La frontière du domaine \(D\) munie d'une telle orientation sera désignée par \(\partial D\).

(Le théorème de Jordan affirme que le complémentaire d'un lacet simple de \(\C\) possède exactement deux composantes connexes, l'une bornée et l'autre non. Nous avons utilisé ce théorème dans la description précédente.)

Soit \(f\) une fonction holomorphe sur \(\bar D\) (au sens où \(f\) se prolonge en une fonction holomorphe sur un domaine \(G \supset \bar D\)). Montrer que l'intégrale de \(f\) le long de la frontière de \(D\) est nulle:
\[\int_{\partial D} f \, dz = \int_{\gamma_0} f \, dz + \sum_{1 \leq \nu \leq n} \int_{\gamma_\nu} f\, dz =0.\]

Soient \(\gamma\) un lacet dérivable et \(f : \gamma \to \R\) une fonction continue (ou intégrable). Montrer que la fonction
\[F(z) = \frac{1}{2\pi i} \int_\gamma \frac{f(\zeta)}{\zeta-z} \, d\zeta\]
est une fonction holomorphe dans \(\hat\C \setminus \gamma\) et nulle à l'infini.

On définit l'indice d'un lacet \(\gamma : [\alpha,\beta] \to \C\) en un point \(z \in \Omega = \C \setminus \gamma\) par la formule:
\[\operatorname{ind}_\gamma(z) =\frac{1}{i2\pi} \int_\gamma \frac{d\zeta}{\zeta-z}.\]

Montrer que

1. \(\operatorname{ind}_\gamma(z)\) est un entier ;
   
2. \(\operatorname{ind}_\gamma\) est constant sur chaque composante connexe de \(\Omega\) ;
   
3. \(\operatorname{ind}_\gamma\) est nul sur la composante connexe non bornée de \(\Omega\).
   

Pourquoi la fonction \(\sum_{n \geq 0} \frac{x^2}{n^2 x^2+1} \), qui converge pour tout \(x \in \R\), ne peut être développée en série de Taylor au voisinage de \(z=0\).